Die analytische Bestimmung des horizontalen radialen Kraftangriffspunktes am Kegel des Kreiselbrechers

1 Einleitung

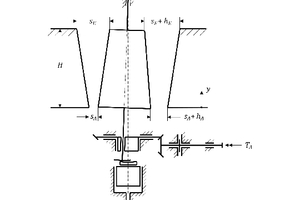
Kreiselbrecher, auch Grobkreisel-, Steilkegel-, Rund-, Konus-, Kurzhubkegel- oder Gates-Typ-Brecher [3; 4; 5; 11] genannt, kommen in Rohstoffgewinnungsbetrieben (Bergwerke, Steinbrüche) als Primärbrecher zum Einsatz, wenn große Durchsatzmengen sprödbrechender Gesteine oder Erze zerkleinert werden müssen (Bild 1). In Sonderfällen werden diese Brecher auch als Sekundär- und Tertiärbrecher eingesetzt. Die Zerkleinerung erfolgt in einem ringförmigen Brechraum, der sich aus einem taumelnden, nach oben sich verjüngenden Brechkegel und einem feststehenden, nach oben sich erweiternden kegelförmigen Brechmantel bildet.

Das Aufgabegut wird zwischen dem den Brechmantel sich periodisch nähernden Brechkegel zerkleinert (Bild 2), während bei sich öffnendem Brechraum das Brechgut weiter nach unten fällt oder gleitet und schließlich aus dem Brechraum ausfällt. Das Brechgut durchläuft vertikal den Brechraum quasi stufenförmig und unterliegt zyklisch Zerkleinerungs-, Transport- und Klassiervorgängen.

Die Dimensionierung dieser Brecher basiert auf unterschiedlichen Methoden. Ziele sind angestrebte Leistungsdaten, wie Durchsatz oder Produktkorngröße, aber auch eine ausreichende Antriebsleistung und mechanische Festigkeit der Maschine unter Beachtung der Charakteristika des Aufgabegutes wie dessen Festigkeit, Korngrößen- und Kornformverteilung. Die dabei angewendeten Methoden lassen sich grob in drei Gruppen einteilen, wie die Nutzung von aus in der Praxis gewonnenen empirischen oder von Hypothesen abgeleiteten Kennzahlen oder Auslegungsdiagrammen [3; 13], die Anwendung von analytischen [2; 11] und numerischen Methoden [1; 6]. Jede dieser Methoden ermöglicht eine Dimensionierung, wenngleich die Aussagekraft unterschiedlich ist. Die Vorgänge im Brechraum ändern sich grundsätzlich stets sowohl örtlich als auch zeitlich. Es liegt gewissermaßen eine doppelte „Diskretisierung“ der Prozesse vor. Die Erfassung dieser Vorgänge ermöglichen numerische Methoden, z.B. DEM. Die Nachteile liegen jedoch in der Bestimmung der vielen Parameter, die zum Teil aufwändig, teilweise auch nicht zu bestimmen sind und nur geschätzt werden können sowie in der Beurteilung zeitlich längerer Zeiträume. Die empirischen und auf Hypothesen basierenden Methoden ermöglichen zwar keine „Diskretisierung“, sie haben aber den großen Vorteil, dass aus einfach zu gewinnenden Messergebnissen praxisrelevante Auslegungsgrößen abgeleitet werden können. Die analytischen Methoden können zwar die Prozesse im Brechraum stufenweise abbilden, eine in der Realität auftretende „Diskretisierung“ jedoch nicht. Gegenüber den kenngrößenbasierten Methoden haben die analytischen Methoden den Vorteil, dass funktionale Zusammenhänge entwickelt und bewertet werden können. Deshalb wird in dieser Abhandlung die analytische Methode gewählt.

Die Bestimmung des erforderlichen Antriebsmomentes und der Antriebsleistung basiert entscheidend auf den Lastannahmen am Brechkegel. Im Folgenden werden daher die radialen Lastannahmen bestimmt und diskutiert. Dazu wird ein vereinfachtes Modell zunächst erstellt und dann hinsichtlich des radialen Kraftangriffspunktes diskutiert und plausibilisiert.

2 Funktionsweise

Der Brechraum eines Kreiselbrechers ist nach oben und unten offen und wird radial vom Brechmantel und Brechkegel begrenzt. Je nach Bauart ändert sich periodisch die Lage des Brechmantels und des Brechkegels. Diese Abhandlung nimmt Bezug auf die am weitesten verbreitete Bauart. Der Brechmantel ist ortsfest und der Brechkegel führt eine taumelnde Bewegung aus, die oben durch ein Kopflager und unten durch eine Exzenterwelle kinematisch bestimmt ist. Im Idealfall dreht sich der Brechkegel nicht um die eigene Achse. In der Praxis führt der Kegel jedoch Ausgleichsbewegungen um die eigene Achse aus (siehe Bild 3).

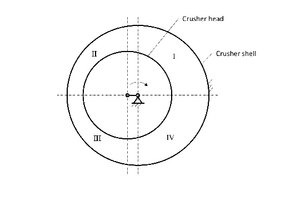
Der Brechraum kann im Querschnitt in vier Sektoren eingeteilt werden.

Er besteht aus zwei sich drehenden, symmetrischen, spiegelbildlich angeordneten sichelförmigen Querschnitten (Bild 4). Im sich in Drehrichtung verengenden Spalt (Sektoren I und II) erfolgt die Zerkleinerung des Gutes, im sich erweiternden Spalt (Sektoren III und IV) der Ausfall. In vertikaler Richtung durchläuft das Brechgut von oben mit dem größten Spalt und den kleinsten radialen Bewegungen nach unten und wird schrittweise in Richtung Austrag zerkleinert, wo der kleinste Spalt, aber der größte Hub ist. Die beim Taumeln sich ändernde, aber mit jeder Umdrehung periodisch sich wiederholende Brechraumgeometrie sowie die Drehzahl müssen so aufeinander abgestimmt sein, dass zwar eine Verdichtung und Zerkleinerung des Brechgutes lokal im Brechraum stattfinden kann, sich jedoch keine Festkörperbrücken über lokal komplett kompaktiertes Brechgut zwischen Mantel und Kegel ausbilden. Dies würde unmittelbar zum Stillstand des Brechers führen bzw. zur Auslösung der Drehmomentenbegrenzung.

3 Grenzen der Erstellung eines Ersatzmodells

Die Zerkleinerung eines Partikels erfolgt räumlich und zeitlich begrenzt im Brechraum (sog. doppelte „Diskretisierung“). Die Kontaktflächen des Brechkegels mit den Partikeln sind deshalb auch örtlich und zeitlich begrenzt belastet. Werden allerdings die Zerkleinerungsvorgänge der den Brechraum passierenden Partikel über einen längeren Zeitraum betrachtet, wird die Oberfläche des Kegels quasi wie durch eine Flächenlast belastet. Die Flächenlast wirkt wie ein Druck auf die Kegeloberfläche. Sie bildet gewissermaßen ein „Lastengebirge“ auf dem Brechkegel. Idealerweise steigt dabei der Druck in vertikaler Richtung vom Eintrag zum Austrag und in radialer Richtung vom größten zum geringsten Spalt in dem Sichelabschnitt, in dem die Zerkleinerung erfolgt (Sektoren I und II). Der andere Sichelabschnitt (Sektoren III und IV) ist drucklos. In der Praxis weicht dieses Idealbild jedoch ab, da beispielsweise die örtliche Aufgabe, die Festigkeit, die Kornform- und Korngrößenverteilung des Aufgabegutes und des erzeugten Brechgutes im Brechraum variieren oder die Reibkräfte in Umfangsrichtung überschritten werden. Dies führt zu Abweichungen der Druckverteilung sowohl in Umfangsrichtung (Vorgänge in den zwei Sichelabschnitten sind nicht scharf getrennt), als auch in Vertikalrichtung (lokale Verdichtungen führen zu lokalen Druckerhöhungen). Bild 5 zeigt einen Längs- und Querschnitt eines idealisierten „Lastengebirges“.

Die Druckverteilung auf dem Brechkegel unterliegt in der Praxis örtlich und zeitlich Schwankungen. Ein für die Berechnung angenommener „stationärer“ Betrieb des Brechers ist also nicht gegeben. Allein die Materialschwankungen, die ständig wechselnde Granulometrie des Aufgabegutes und die schrittweise Zerkleinerung im Brechraum verhindern prinzipiell die Entwicklung eines „stationären“ Betriebs. Diese Schwierigkeiten zeigen auf, dass es auch nicht die eine Berechnungsmethode gibt. Aus diesem Grund soll ein Ersatzmodell entwickelt werden, dessen Ergebnisse in einer Bandbreite vorliegen. Die Methode muss deshalb die Erkennbarkeit funktionaler Abhängigkeiten zwischen geometrischen und physikalischen Parametern ermöglichen. Dadurch kann durch Parametervariation deren Einfluss auf den hier zu ermittelnden Angriffspunkt der resultierenden Brechkraft auf den Kegel abgeschätzt werden. Ebenso können Extremfälle eingeordnet und diskutiert werden.

4 Formulierung des Ersatzmodells

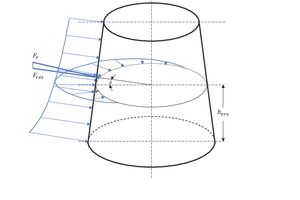
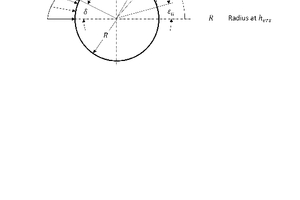
Das Ersatzmodell geht von einer idealen Kegelgestalt des Brechkegels und des Brechmantels aus. Die auf den Kegel wirkende Flächenlast kann durch eine resultierende Ersatzkraft F_r zusammengefasst werden (Bild 5). Für die Berechnung des Angriffspunktes ist die horizontale Kraftkomponente F_res ausschlaggebend. Dabei wird angenommen, dass die radiale Druckverteilung auf dem Brechkegel zunächst über die gesamte Höhe qualitativ, aber nicht quantitativ gleich ist (siehe hierzu Kapitel 6. Diskussion und Einordnung der Ergebnisse). Sie kann deshalb durch eine Linienlast p(ε) repräsentiert werden. Die horizontale Ersatzkraft F_res wirkt dann in Höhe h_ers und in Umfangsrichtung am Winkel δ auf den Kegel (Bild 5). Die Verhältnisse im Brechraumquerschnitt auf der Höhe h_ers sind im Bild 6 verdeutlicht.

Die Exzentrizität r zwischen Mantel- und Kegelmittelachse bestimmt den Hub h und damit den engsten Spalt s (Englisch: closed side setting CSS) und den größten Spalt s + h (Englisch: open side setting OSS), wobei h = 2r ist. Der Mittelpunkt O_K des Kegels dreht sich dabei um den Mittelpunkt O_M des Mantels, ohne dass der Kegel sich idealerweise um die eigene Achse O_K dreht. Zu beachten ist, dass alle Größen sich auf die Höhe h_ers beziehen und nicht auf die Höhe der Brechgutaufgabe bzw. des Brechgutaustrags oder der Exzenterbuchse.

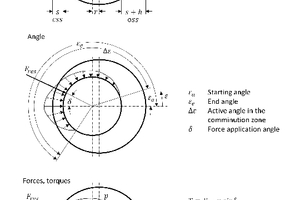
Das Brechgut wird im Bereich des größten Spaltes aufgegeben und dann durch Bewegung des Brechkegels zerkleinert. Nach Passieren des engsten Spaltes kann das Brechgut ausfallen. Die Linienlastentwicklung p(ε) steigt mit dem sich reduzierenden Spalt und fällt dann wieder bei sich erweiterndem Spalt. Der Druckanstieg beginnt im Sektor I beim Winkel ε_a. Der Kegel ist dann wieder drucklos im Sektor III nach einem Winkel Δε bei ε_e. Der resultierende Kraftangriffswinkel δ liegt versetzt nahe dem engsten Spalt. Die resultierende Ersatzkraft F_res bildet einen Hebelarm von r sin δ zum Antrieb des Kegels. Damit kann das Antriebsmoment T und mit der Drehzahl n des Mittelpunktes O_K des Kegels um den Mittelpunkt des Mantels O_M die Antriebsleistung P berechnet werden. Bei Berücksichtigung der Verluste und der geometrischen Verhältnisse können so das Antriebsmoment und die Antriebsleistung der Exzenterbuchse und dann des Antriebsmotors ausgelegt werden.

Das in dieser Abhandlung erstellte Ersatzmodell geht nun davon aus, dass im Sektor III keine Radialkraft mehr auftritt. Der Druck im Spalt steigt stetig in Umfangsrichtung vom größten zum kleinsten Spalt in den Sektoren I und II. Unter diesen Voraussetzungen ergibt sich folgendes Ersatzbild (Bild 7):

Die Linienlast p(ε) wirkt demnach im Winkelbereich von ε_a bis ε_e = π und der funktionale Zusammenhang mit dem Wirkwinkel ε folgt allgemein einer exponentiellen Funktion:

⇥(1)

mit einer charakteristischen Größe, der Einheitslinienlast p₀ und dem Exponenten n (siehe auch [7]).

5 Berechnung der resultierenden Ersatzkraft und deren Angriffspunkt

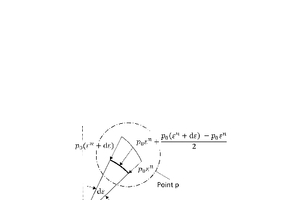
Die Linienlast p wirkt im Winkelbereich ε_a bis π. Die resultierende Kraft F_res ergibt sich aus dem Integral der Linienlast p(ε) über das Umfangsteilstück, das von den Winkeln ε_a und π gebildet wird (Bild 8).

An einem infinitesimal kleinen Umfangsabschnitt Rdε wirkt bei einem Winkel ε die Last p₀εⁿ und bei dem Winkel ε + dε die Last p₀(εⁿ + dε), im Mittel dann  .

Für den mit Linienlast beaufschlagten Winkelbereich dε gilt dann die resultierende Linienlast p_L:

⇥(2)

⇥(3)

Da (dε)² << dε kann (dε)² vernachlässigt werden, so dass

⇥(4)

Für die resultierende Kraft ergibt sich:

⇥(5)

⇥(6)

⇥(7)

Zur Bestimmung des Kraftangriffswinkels δ gilt, dass die Aufsummierungen, d.h. die Integrale der Linienlasten p_L von ε = ε_a bis π - δ und ε = π – δ bis π gleich sein müssen:

⇥(8)

Daraus folgt

⇥(9)

bzw.

⇥(10)

und dann die Bestimmungsgleichung für δ

⇥(11)

Für den einfachen Sonderfall n = 1 und ε_a = 0 gilt für die resultierende Ersatzkraft F_res

⇥(12)

sowie mit der Beziehung (11)

⇥ (13)

der Winkel δ

⇥ (14)

oder

δ = 52,72°⇥(15)

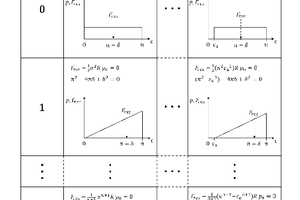
Der Startwinkel ε_a der Linienlastentwicklung p(ε) kann variieren, ebenso der Exponent n. Tabelle 1 gibt eine Übersicht der Bestimmungsgleichungen und der qualitativen Verläufe der Linienlastentwicklungen p(ε). Je nach Winkel ε_a und Exponent n liegt der Angriffspunkt bei einem anderen Winkel δ. Ergänzend sind die Bestimmungsgleichungen für die resultierende Kraft F_res und der Einheitslinienlast p₀ angegeben. Die Auswertung kann in zweierlei Hinsicht erfolgen. Wird p₀ als konstant angesehen, ändert sich die resultierende Kraft F_res entsprechend der Bestimmungsgleichungen. Bei konstanter resultierender Kraft F_res ändert sich auch der Kurvenverlauf von p(ε) aufgrund der Änderung von p₀. Die entsprechenden Winkel δ bleiben aber bestehen.

In Tabelle 2 erfolgt dann die Auswertung für den Kraftangriffswinkel δ bei unterschiedlichen Startwinkeln ε_a und Exponenten n. Zur besseren Ablesbarkeit der Werte wurde die Form einer Matrix mit Zahlenwerten gewählt.

Der Kraftangriffswinkel δ hängt somit von der Zerkleinerungszone ε_a bis ε_e und dem Exponenten n der Linienlastentwicklung p(ε) ab. Der Einfluss auf den Winkel δ ist umso kleiner, je kleiner die Zerkleinerungszone ε_a bis ε_eund je größer der Exponent n ist. Bei gut gefüllten Brechräumen und bei überschütteter Brechgutaufgabe liegen die Anfangswinkel ε_a bei 0° bis maximal 30°. Größere Anfangswinkel sind bei schlecht gefüllten Brechräumen und einzelnen Aufgabebrocken zu beobachten.

6 Diskussion und Einordnung der Ergebnisse

Der Kraftangriffswinkel δ ist eine Systemeigenschaft. Das System wird durch Eigenschaften der Maschine, des Brechgutes, der Aufgabe und deren Wechselwirkungen charakterisiert.

Während Material, Geometrie und Kinematik des Brechers gegeben und definiert sind und nur in engen Grenzen oder durch Umbau geändert werden können, wie Hub, Spalt, Drehzahl oder Kontur des Kegels, kann das Brechgut in weiten Bereichen variieren, selbst innerhalb einer Lagerstätte.

Die wichtigsten Zerkleinerungseigenschaften des Brechgutes lassen sich in zwei Gruppen einteilen, die sich teilweise gegenseitig beeinflussen. Die erste Gruppe umfasst stoffliche Eigenschaften, wie das Bruchverhalten (spröd oder duktil), die Festigkeit (Druck-, Biegefestigkeit, Point-Load-Index) und die Gefügeeigenschaften (Modus, Struktur, Textur) des Brechgutes. Die zweite Gruppe bezieht sich auf geometrische Eigenschaften, wie die Korngrößen- und Kornformverteilung des Brechgutes. Zu beachten ist, dass manche Eigenschaften durch physikalische Effekte gekoppelt sind, wie der Größen- und Formeinfluss der Körner auf die Festigkeitseigenschaften.

Einen entscheidenden Einfluss auf den Kraftangriffswinkel hat auch die Art und Anordnung der Brechgutaufgabe in den Kreiselbrecher. Das Brechgut kann vorklassiert oder auch nicht, bzw. überschüttet oder nicht mit SKW, Band oder Schubwagenspeiser dem Brecher zugeführt werden. Dabei kann das Brechgut ein-, zwei- oder dreiseitig aufgegeben werden.

Schließlich bestehen zahlreiche Wechselwirkungen zwischen den Systemparametern, wie das Lückenvolumen im Brechraum, das die Beweglichkeit der Bruchstücke bestimmt. Der Kraft- und Energieeintrag in die zu zerkleinernden Partikel hängt sowohl von der Kontaktgeometrie zwischen ihnen und den Arbeitsflächen des Brechers als auch von ihrer Orientierung im Brechraum ab.

Für den Kraftangriffswinkel δ sind deshalb lediglich Trendaussagen möglich, da im Betrieb viele Parameter variieren.

Zur Abschätzung des Kraftangriffswinkels wird von sprödem Stoffverhalten ausgegangen. Die meisten in Kreiselbrechern zerkleinerten Stoffe sind sprödbrechend, wie Hartgesteine oder zahlreiche Erze. Charakteristisch für sprödes Stoffverhalten ist eine steile Kraft-Weg-Kurve (σ-ε-Kurve) beim Druckversuch, die mit einem Gewaltbruch schlagartig endet. Erfolgt die Krafteinleitung in ein Brechgutpartikel über seine Ecken oder Kanten, setzt sich die Zerkleinerung zunächst aus vielen Teilbrüchen zusammen, bis das volumenreduzierte Partikel eine Lage einnimmt, in der es größere Kräfte aufnehmen kann. Bei weiterer Kraftzufuhr zerbricht es dann schlagartig [9; 10; 12]. Das Stoffverhalten lässt sich durch die Beziehung (1) der Linienlast p(ε) durch den Exponenten n beschreiben. Bei sprödem Stoffverhalten gilt zunächst:

n » 1 ⇥ (16)

Die Kraft-Weg-Kurven der Partikel sind jedoch auch Systemeigenschaften. Die Kurven in Bild 9 und Bild 10 verdeutlichen exemplarisch das unterschiedliche Zerkleinerungsverhalten eines typischen Hartgesteins (Diorit, Druckfestigkeit 180 bis 240 MPa) aus der Lagerstätte Hohwald/Sachsen [12]. Zwei Diorit-Proben der Fraktion 140/200 mm aus dem Haufwerk eines begrenzten Abschlags wurden in einem Prüfstand durch Druck zerkleinert. Dabei erfolgte die Aufnahme der Kraft-Weg-Kurven p(ε). 

Während Probe Nr. 31 einen Kornformwinkel von 164° und so eine fast komplette flache Auflage des Steins auf den Flächen des Prüfgerätes aufwies, war der Kontakt der Probe Nr. 25 durch einen Kornformwinkel von 128° und damit durch einen Kantenkontakt charakterisiert. Die Probe Nr. 31 zeigt zunächst eine steile Kraftentwicklung, die mit einem Exponenten n » 1 dargestellt werden könnte. Dann weist sie einen Gewaltbruch auf, um anschließend auf relativ hohem Kraftniveau zahlreiche kleinere Bruchereignissen zu zeigen. Dieser Teil der Kurve ließe sich global mit einem Exponenten n = 0 beschreiben. Die Probe Nr. 25 zeigt trendmäßig einen geringer ausfallenden Kraftanstieg. Er ist durch zahlreiche Brüche unterbrochen, die mit fortschreitendem Hub intensiver ausfallen – ein Indiz, dass die Bruchstücke eine flachere Auflagefläche entwickeln. Der trendmäßige Kraftanstieg ließe sich global mit einem Exponenten n = 1 beschreiben.

Die Auswertung von mehr als 600 Diorit-Proben der Fraktionen 25/40 mm bis 450/560 mm der Lagerstätte Hohwald lässt trendmäßig global folgende Aussagen zu: Bis zu einem relativen Hub h_r von 5 % steigt die Kraftentwicklung stark an, um dann bis zu einem relativen Hub h_r von 20/25 % nur noch moderat zu wachsen [12].

Der relative Hub h_r ändert sich längs der Brechraumhöhe eines Kreiselbrechers. Er ist bei der Brechgutaufgabe wesentlich kleiner als beim Austrag. Typischerweise übersteigt der Hub bei der Aufgabe nicht 0,5 bis 1,5 %, während er am Austrag nicht 15 bis 25 % überschreitet. Im oberen Teil des Brechraumes kommt deshalb nur der erste Teil der Kraft-Weg-Kurven zum Tragen. Er ist insbesondere auch durch Einordnungs- und Umorientierungsvorgänge der Brechgutpartikel charakterisiert, so dass hier mit Einzelkornzerkleinerung und zunächst nicht mit vollständiger Brechraumfüllung zu rechnen ist. Im unteren Teil des Brechraumes ist das Brechgut schon vorzerkleinert und vorklassiert und die Brechraumpartikel „durchfahren“ die gesamte Kraft-Weg-Kurve in Folge des größeren Hubes. Der hintere Teil der Kraft-Weg-Kurve überlagert sich deshalb verstärkt mit Verdichtungsvorgängen bis hin im Extremfall zu lokal auftretenden Zerkleinerungsvorgängen im Gutbett. Bezogen auf das Brechgutverhalten bedeutet diese Hubentwicklung längs des Brechraumes, dass die Linienlastentwicklung p(ε) im oberen Teil vornehmlich durch einen Exponenten n > 1 charakterisiert werden kann, während im unteren Teil der Exponent n ≥ 1 ist. Diese Abschätzung wird durch die Beobachtung bei Aufgabe von vorklassiertem Aufgabegut unterstützt. Die Gewichtung zwischen oberem und unterem Brechraum hinsichtlich der Lastentwicklung verschiebt sich in Richtung des oberen Brechraums. Der untere Brechraum wird entlastet. Dies bedeutet, dass der Exponent n für den gesamten Brechraum steigt und somit der Winkel des Kraftangriffspunktes sinkt, mit der Konsequenz eines geringeren Antriebsmomentes und einer verringerten aufgenommenen Antriebsleistung.

Unter Berücksichtigung der Kraft-Weg-Kurven kann mit sich ständig ändernden Exponenten n und damit auch mit sich ebenso ständig ändernden Kraftangriffswinkeln δ gerechnet werden. Die Schwankungen des Antriebmomentes und der aufgenommenen Motorleistung haben ihre Ursache neben etwa solchen der Aufgabemenge auch in dem unterschiedlichen Brechverhalten der Steine des Aufgabegutes.

Für die Auslegung der Kreiselbrecher kann im Mittel mit einem Exponenten n > 1 gerechnet werden. Für den Angriffswinkel δ sollte ein Winkel zwischen 30° und 40° gewählt werden. Bei diesen Winkeln spielt die Größe der Zerkleinerungszone ε_a bis ε_e nur eine untergeordnete Rolle, so dass die Brechgutaufgabe praktisch keinen Einfluss auf den Kraftangriffswinkel δ hat. Nur in Extremfällen bei einseitiger Aufgabe von einzelnen, harten Brocken kann sich der Winkel fasst halbieren. Die resultierende Zerkleinerungskraft F_res wird in diesem Fall jedoch geringer sein.

Eine Literaturauswertung gibt nur wenige Hinweise. Olevskii [8] leitet einen Winkel δ von 5°45‘ ab. Jedoch basiert das Ergebnis auf Lastannahmen in den Sektoren I, II und III. Mölling [5] hingegen fußt die Angabe von δ = 20° auf eine Lastentwicklung im Sektor II über einen Winkelbereich von 40°, ohne jedoch auf die Berechnung oder eine Messung einzugehen. Dieser Winkel δ = 20° wurde auch in einem Buch [3] zu Zerkleinerungs- und Klassiermaschinen übernommen.

Zusammenfassend kann für die Auslegung von Kreiselbrechern ein Kraftangriffswinkel δ von etwa 30° bis 40° ausgegangen werden, sofern das Brechgut sprödes Stoffverhalten aufweist. Bei der Zerkleinerung von wenigem Brechgut im Brechraum kann der Kraftangriffswinkel δ auf fast halbierte Werte sinken. Für die Berechnung des Antriebsmomentes und der -leistung sind diese Werte allerdings nur im Ausnahmefall von einzelnen hochfesten Stücken im Brechraum relevant. Eine Validierung des abgeleiteten Kraftangriffswinkels δ kann durch Messungen an Kreiselbrechern ermöglicht werden.